
Fundamentos de Teoría de la Música
En este nivel se explican las notas musicales, los intervalos, las escalas Mayores y menores, y la Tonalidad.
La Rueda Armónica permite obtener fácilmente el intervalo existente entre dos notas cualesquiera, así como las notas que constituyen cualquier escala Mayor o menor, ya sea ésta natural, armónica o melódica, junto con su armadura correspondiente. Como novedad, la Rueda Armónica aporta una visión completa y panorámica de las relaciones existentes entre todas las tonalidades.
Así como el ciclo de quintas muestra las tonalidades en una línea (una dimensión), la Rueda Armónica las muestra en una superficie (es decir, en dos dimensiones). De esta manera se aprecian, además del ciclo de quintas, los cambios de modo, los cuales no son visibles en el ciclo de quintas. Se tiene, de esta manera, un verdadero mapa de las tonalidades.
1. NOTAS MUSICALES
Las Notas Musicales son 12, de las cuales 7 son naturales y 5 son alteradas. Las notas naturales, ordenadas según su altura, de la más grave a la más aguda (coloquialmente, de la más “baja” a la más “alta”), son: Do, Re, Mi, Fa, Sol, La y Si. Estas 7 notas forman la denominada Escala de Do Mayor y se corresponden con las “teclas blancas” del piano. A continuación del Si viene otro Do y así sucesivamente. Ahora bien, el primer y el segundo Do no son idénticos, ya que el segundo tiene mayor altura que el primero.
Lo que ocurre es que, físicamente, la “frecuencia de vibración” del segundo es justamente el doble de la del primero, lo que hace que estas dos notas se perciban como muy “afines” entre sí, hasta el punto de asignarles el mismo nombre. Se dice que están a distancia de una octava, debido a que hay 8 notas naturales desde el primer Do hasta el segundo Do, contando tanto la nota inicial como la final.
La distancia entre dos notas naturales consecutivas no es siempre la misma, sino que en algunos casos hay una distancia de Tono (T) y en otros de medio tono o Semitono (S). En concreto, entre Mi y Fa hay un semitono, al igual que entre Si y Do. En cambio, entre las demás notas naturales consecutivas hay un tono. Por este motivo, entre ellas se intercalan las denominadas notas alteradas, a distancia de semitono, las cuales se corresponden con las “teclas negras” del piano (figura 1). De este modo resulta un conjunto de 12 notas diferentes, existiendo siempre un semitono entre cada nota y la siguiente. La distancia entre un Do y su octava (es decir, el siguiente Do) será, por tanto, de 12 S ó 6 T. Este conjunto de 12 notas se conoce como Escala Cromática.
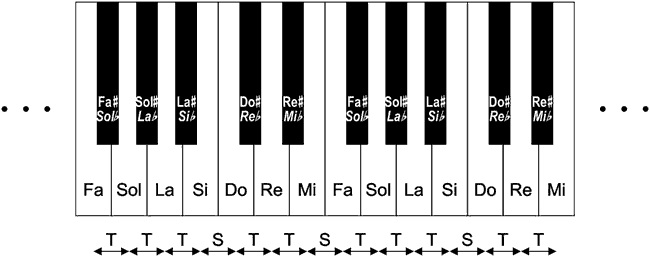
Figura 1. Las notas musicales y su localización en el piano.
Para nombrar las notas alteradas se utiliza el sostenido (♯), que sube la nota un semitono, y el bemol (♭), que baja la nota un semitono. Así, por ejemplo, entre Do y Re (donde hay una distancia de un tono) se intercala otra nota a mitad de altura entre ambas, que puede llamarse Do♯ o Re♭. Estas dos notas, que tienen distinto nombre pero el mismo sonido, se dice que son enarmónicas. También son enarmónicas, por ejemplo, el Mi♯ y el Fa natural o el Si natural y el Do♭ (la denominación “natural” significa “sin ninguna alteración”). En ocasiones se utiliza el doble sostenido (![]() ) o el doble bemol (
) o el doble bemol (![]() ) para subir o bajar la nota un tono, respectivamente.
) para subir o bajar la nota un tono, respectivamente.
Pese a que las 12 notas están uniformemente espaciadas, en la figura 1 puede apreciarse claramente el diferente tratamiento que se da a las notas naturales y a las alteradas, así como la falta de uniformidad que existe en la distribución de tonos y semitonos entre las notas naturales. Todo esto, que puede parecer extraño y caprichoso, no es sino el resultado de siglos de evolución de la teoría musical, lo que a su vez es consecuencia de las relaciones de afinidad que existen entre los sonidos, así como de la gran cohesión y unidad que presenta el conjunto de 7 notas de la escala Mayor.
Además, como se verá en el Capítulo 5, una Escala Mayor puede construirse comenzando por cualquiera de las 12 notas, dando lugar a las escalas de Re Mayor, La♭ Mayor, etc., lo que hace que las 12 notas sean igualmente importantes. La escala de Do Mayor es, simplemente, la que tiene todas sus notas naturales. En la Guitarra, por ejemplo, las 12 notas tienen exactamente el mismo tratamiento (figura 2).

Figura 2. Disposición de las notas en la 3ª cuerda de la Guitarra.
2. INTERVALOS
Se llama Intervalo a la distancia en altura entre dos notas cualesquiera, la cual viene determinada por el número de tonos o semitonos que haya entre ellas. Este número, sin embargo, no indica el grado de afinidad que existe entre las dos notas ni su lugar relativo dentro de una escala Mayor. Por ello, lo más habitual es indicar el intervalo mediante un número ordinal y un calificativo. El número ordinal indica el número de notas naturales que hay desde la nota inicial a la nota final, incluyendo ambas. Y, a menos que se indique lo contrario, se entenderá que el intervalo es ascendente, es decir, que la segunda nota es más aguda que la primera. Así, por ejemplo, “de Re a La” hay un intervalo de 5ª (Re – Mi – Fa – Sol – La son 5 notas naturales en sentido ascendente).
Si consideramos ahora el intervalo de Re♯ a La♭, tenemos también una 5ª (Re – Mi – Fa – Sol – La son 5 notas naturales en sentido ascendente), aunque la distancia es menor que entre Re y La. Para tener en cuenta estas diferencias se añade al ordinal un calificativo relacionado con el número de tonos y semitonos que contiene el intervalo. La calificación de los intervalos está basada en la escala Mayor. Así, todos los intervalos que se producen desde el Do grave hasta cualquier otra nota de la escala de Do Mayor en sentido ascendente se llaman Mayores (M) o Justos (J). Concretamente, entre el Do y las notas Fa, Sol y Do, el intervalo se llama Justo, mientras que entre el Do y las demás notas de esta escala el intervalo se llama Mayor (en el Capítulo 3 se dará una explicación de esto). La tabla 1 muestra estos intervalos e indica, además, el número de tonos que contiene cada uno de ellos.
| De Do a |
Do |
Re |
Mi |
Fa |
Sol |
La |
Si |
Do |
|
Intervalo |
1ª J |
2ª M |
3ª M |
4ª J |
5ª J |
6ª M |
7ª M |
8ª J |
|
Distancia en Tonos |
0 |
1 |
2 |
2,5 |
3,5 |
4,5 |
5,5 |
6 |
Tabla 1. Intervalos en la escala de Do Mayor ascendente.
El intervalo de 1ª J se denomina Unísono y el de 8ª J suele llamarse, simplemente, Octava. Para referirnos a otros intervalos diferentes a los anteriores, se utilizan los siguientes calificativos:
- Menor (m), si tiene un semitono menos que el Mayor. Por ejemplo, de Do a Mi♭ habrá una 3ª m (1,5 T) y de Do a Si♭ una 7ª m (5 T).
- Aumentado (A), si tiene un semitono más que el Mayor o el Justo. Por ejemplo, de Do a Re♯ hay una 2ª A (1,5 T), de Do a Fa♯ una 4ª A (3 T) y de Do a La♯ hay una 6ª A (5 T).
- Disminuido (d), si tiene un semitono menos que el menor o el Justo. Por ejemplo, de Do a Sol♭ hay una 5ª d (3 T) y de Do a Si
 hay una 7ª d (4,5 T).
hay una 7ª d (4,5 T). - Cuando resulta necesario se emplea el término doble Aumentado (AA) para el intervalo que tiene un semitono más que el Aumentado, y el término doble disminuido (dd) para el intervalo que tiene un semitono menos que el disminuido.
| De Do a |
Do♯ |
Re♭ |
Re♯ |
Mi♭ |
Fa♯ |
Sol♭ |
Sol♯ |
La♭ |
La♯ |
Si♭ |
|
Intervalo |
1ª A |
2ª m |
2ª A |
3ª m |
4ª A |
5ª d |
5ª A |
6ª m |
6ª A |
7ª m |
|
Distancia en Tonos |
0,5 |
0,5 |
1,5 |
1,5 |
3 |
3 |
4 |
4 |
5 |
5 |
Tabla 2. Intervalos de Do a las notas alteradas.
Las dos filas inferiores de la tabla 1 sirven también para determinar el intervalo existente entre dos notas cualesquiera, sin necesidad de que la primera de ellas sea un Do. Veamos algunos ejemplos:
- De Re a La hay un intervalo de 5ª (Re – Mi – Fa – Sol – La son 5 notas naturales en sentido ascendente) que tiene 3,5 T. Es, por tanto, una 5ª J.
- De Re♯ a La♭hay también una 5ª, pero ésta tiene 2,5 T, por lo que se trata de una 5ª dd.
- De Si♭ a Sol♯ hay un intervalo de 6ª que tiene 5 T. Es, por tanto, una 6ª A.
- De La♭ a Do
 hay una 3ª que tiene 3 T, por lo que se trata de una 3ª AA.
hay una 3ª que tiene 3 T, por lo que se trata de una 3ª AA.
Los intervalos que no superan una octava, como los vistos hasta ahora, se denominan simples, mientras que los que sí la superan se denominan compuestos. Estos últimos siempre pueden reducirse a simples eliminado el número de octavas necesario. El calificativo que se aplica a los intervalos compuestos es el mismo que tendrían si los redujéramos a simples.
3. INVERSIÓN DE INTERVALOS
La inversión del intervalo consiste, simplemente, en invertir el orden de las notas que lo forman. Así, si invertimos el intervalo Re – La, que es una 5ª J, resulta el intervalo La – Re, que es una 4ª J. Y si invertimos el intervalo Mi – Sol♯, que es una 3ª M, resulta el intervalo Sol♯ – Mi, que es una 6ª m. En la inversión del intervalo se cumplen siempre las dos reglas siguientes:
- La suma de los números correspondientes a un intervalo simple y a su inversión es siempre 9.
- En la inversión del intervalo, el Mayor se convierte en menor, el menor en Mayor, el Aumentado en disminuido, el disminuido en Aumentado, el doble Aumentado en doble disminuido y el doble disminuido en doble Aumentado. El Justo, sin embargo, permanece Justo.
En la práctica, la inversión del intervalo se consigue elevando la nota inferior una octava o bajando la nota superior una octava. Pero al mismo resultado se llega si invertimos el sentido ascendente del intervalo en descendente. Así, de Re a La hay 5 notas naturales en sentido ascendente (Re – Mi – Fa – Sol – La) y una distancia de 3,5 T, por lo que es una 5ª J. Pero, en sentido descendente, hay 4 notas naturales (Re – Do – Si – La) y una distancia de 2,5 T, es decir, una 4ª J. Luego la inversión del intervalo puede interpretarse de estas dos formas diferentes.
Resulta ilustrativo comprobar que, en la escala descendente de Do Mayor, todos los intervalos que se producen desde el Do agudo hasta cualquier otra nota de la escala son menores (m) o Justos (J). La tabla 3 muestra estos intervalos e indica, además, el número de tonos que contiene cada uno de ellos.
| De Do a |
Do |
Si |
La |
Sol |
Fa |
Mi |
Re |
Do |
|
Intervalo |
1ª J |
2ª m |
3ª m |
4ª J |
5ª J |
6ª m |
7ª m |
8ª J |
|
Distancia en Tonos |
0 |
0,5 |
1,5 |
2,5 |
3,5 |
4 |
5 |
6 |
Tabla 3. Intervalos en la escala de Do Mayor descendente.
Si comparamos esta tabla con la tabla 1 del Capítulo 2, observamos que, aparte de los intervalos de 1ª y 8ª, los de 4ª y 5ª son los únicos que tienen el mismo número de tonos y semitonos en la escala ascendente y en la descendente. Por otra parte, las notas Fa y Sol guardan una gran afinidad con la nota Do, lo que es consecuencia de las relaciones de frecuencia que hay entre estas notas desde el punto de vista físico. Todo ello hace que estos intervalos se califiquen de “Justos”. Recuérdese que los intervalos de 4ª J y 5ª J son uno el inverso del otro.
Aunque en menor medida, también guardan una gran afinidad con la nota Do aquellas notas que se encuentran a distancia de 3ª M o 3ª m, así como sus correspondientes inversiones, a distancias de 6ª m o 6ª M, respectivamente. Esta idea de afinidad a que hemos aludido varias veces recibe el nombre de Consonancia y está relacionada con el fenómeno físico de la vibración que da lugar al sonido. Como resumen diremos que, aparte del unísono y la octava, los Intervalos Consonantes son la 5ª J, la 3ª M y la 3ª m, junto con sus inversiones, la 4ª J, la 6ª m y la 6ª M, respectivamente. Los demás intervalos son Disonantes. Desde el punto de vista práctico, esto significa que, si se perciben simultáneamente dos notas que forman un intervalo consonante, resulta una sensación de armonía, reposo y estabilidad. Por el contrario, la percepción simultánea de dos notas que forman un intervalo disonante produce una sensación de tensión e inestabilidad.
Por último, en las tablas 1 y 3 también observamos que aparecen todas las distancias interválicas salvo la de 3 T o Tritono, intervalo altamente disonante y con unas características especiales. En realidad, con las notas de la escala de Do Mayor sólo encontramos un intervalo de tritono en Fa – Si (4ª A) o en su inversión Si – Fa (5ª d).
El concepto de Octava y su división en 12 partes, el concepto de Consonancia y el concepto de Escala Mayor son 3 principios fundamentales en los que se basa toda la Música occidental, independientemente del estilo musical considerado.
4. INTERVALOS Y RUEDA ARMÓNICA
El determinar qué intervalo hay entre dos notas cualesquiera es una de las primeras complicaciones que surgen cuando uno comienza el estudio de la Música. Sin embargo, esta tarea se simplifica notablemente utilizando la Rueda Armónica. En este capítulo vamos a ver cómo. En la Rueda Armónica, las Notas Musicales se han representado en COLOR NEGRO y las parejas de notas enarmónicas se han representado poniendo una nota justo encima de la otra. Por otra parte, las notas se han colocado de manera que cada nota está conectada, mediante líneas rojas, con las 6 notas con las que forma Intervalos Consonantes.
Como se ha explicado previamente, los Intervalos Consonantes son combinaciones de 2 notas que, tocadas simultáneamente, producen una sensación de armonía, reposo y estabilidad. Y, aparte del unísono y la octava, son la 5ª J, la 3ª M y la 3ª m, así como sus inversiones. En la Rueda Armónica, cada uno de estos intervalos consonantes se ha representado mediante un tipo de línea diferente. Así, se han usado Circunferencias para los intervalos de 5ª J (y su inversión, la 4ª J); Radios, para los de 3ª m (y su inversión, la 6ª M); y Espirales, para los de 3ª M (y su inversión, la 6ª m). En la figura 3 pueden verse estos tres tipos de líneas.
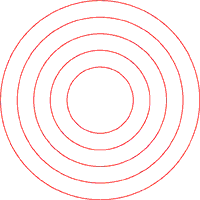
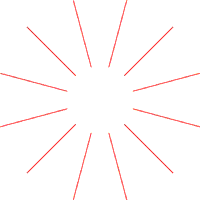

Circunferencias: 4ª J, 5ª J | Radios: 3ª m, 6ª M | Espirales: 3ª M, 6ª m
Figura 3. Líneas empleadas para representar los intervalos consonantes.
Como ejemplo, en la figura 4 puede verse la nota Mi y las 6 notas con las que forma intervalos consonantes, que son:
- La y Si, a intervalos de 4ª J y 5ª J, respectivamente, y situadas en la circunferencia que pasa por la nota Mi. Si recorremos la circunferencia hacia la derecha tenemos intervalos de 5ª J y, si la recorremos hacia la izquierda, de 4ª J. (Descartamos la enarmonía Do♭ porque no forma con Mi un intervalo de 5ª, sino de 6ª).
- Sol y Do♯, a intervalos de 3ª m y 6ª M, respectivamente, y situadas en el radio que pasa por la nota Mi. Si recorremos el radio hacia arriba tenemos intervalos de 6ª M y, si lo recorremos hacia abajo, de 3ª m. (Descartamos la enarmonía Re♭ porque no forma con Mi un intervalo de 6ª, sino de 7ª).
- Do y Sol♯, a intervalos de 6ª m y 3ª M, respectivamente, y situadas en la espiral que pasa por la nota Mi. Si recorremos la espiral hacia la derecha tenemos intervalos de 3ª M y, si la recorremos hacia la izquierda, de 6ª m. (Descartamos la enarmonía La♭ porque no forma con Mi un intervalo de 3ª, sino de 4ª).
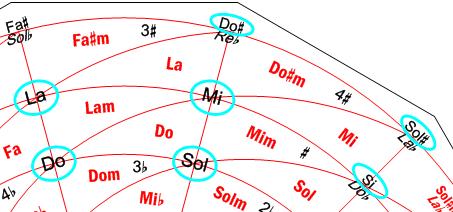
Figura 4. La nota Mi y las 6 notas con las que forma intervalos consonantes.
NOTA: Todas las indicaciones realizadas en COLOR AZUL CLARO se han incluido con fines ilustrativos y no aparecen en la Rueda Armónica.
Estos 3 tipos de líneas nos permiten, además, conocer de forma sencilla qué intervalo hay entre dos notas cualesquiera. Para ello, basta con que nos fijemos en los intervalos Mayores (de 3ª y 6ª) y Justos (de 4ª y 5ª). Las direcciones en que se encuentran estos intervalos con respecto a una nota cualquiera son siempre las mismas y son fáciles de memorizar. En la figura 5 se han señalado estos intervalos a partir de la nota Mi.
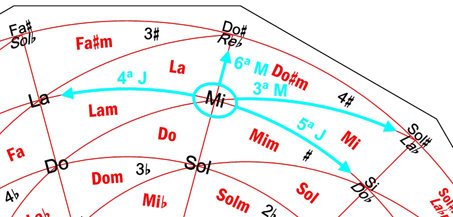
Figura 5. Intervalos de 3ª M, 4ª J, 5ª J y 6ª M a partir de la nota Mi.
Por comparación con estos 4 intervalos podemos determinar qué intervalo forma la nota Mi con cualquier otra, salvo si se trata de una 2ª o su inversión, una 7ª. Pero, para estos dos casos, basta con recordar que el intervalo de 2ª M tiene 1 T. El procedimiento a seguir consiste en determinar, en primer lugar, el número ordinal del intervalo buscado y, en segundo lugar, su calificativo. Si seguimos este orden, no tendremos que preocuparnos de las enarmonías que puedan aparecer. Veamos algunos ejemplos:
¿Qué intervalo hay de Mi a Sol?
Es una 3ª. Por tanto, seguimos la línea de la 3ª M y comparamos con el Sol que hay en su extremo.
Como éste es un Sol♯, eso significa que de Mi a Sol♯ hay una 3ª M, por lo que de Mi a Sol habrá una 3ª m.
¿Qué intervalo hay de Mi a Do?
Es una 6ª. Por tanto, seguimos la línea de la 6ª M y comparamos con el Do que hay en su extremo.
Como éste es un Do♯, eso significa que de Mi a Do♯ hay una 6ª M, por lo que de Mi a Do habrá una 6ª m.
¿Qué intervalo hay de Mi a Si♭?
Es una 5ª. Por tanto, seguimos la línea de la 5ª J y comparamos con el Si que hay en su extremo.
Como éste es un Si natural, eso significa que de Mi a Si hay una 5ª J, por lo que de Mi a Si♭ habrá una 5ª d.
¿Qué intervalo hay de Mi a La♯?
Es una 4ª. Por tanto, seguimos la línea de la 4ª J y comparamos con el La que hay en su extremo.
Como éste es un La natural, eso significa que de Mi a La hay una 4ª J, por lo que de Mi a La♯ habrá una 4ª A.
¿Qué intervalo hay de Mi a Re♯?
Es una 7ª. Su inversión, de Re♯ a Mi, tiene 0,5 T, por lo que éste es un intervalo de 2ª m.
Por tanto, de Mi a Re♯ habrá una 7ª M.
Comenzamos considerando el intervalo de Mi a Sol♯, que es una 3ª.
Y, siguiendo el procedimiento anterior, vemos que es una 3ª M. Por tanto, de Mi♭ a Sol♯ habrá una 3ª A.
¿Qué intervalo hay de Mi♯ a La♭ ?
Comenzamos considerando el intervalo de Mi a La♭, que es una 4ª.
Y, siguiendo el procedimiento anterior, vemos que es una 4ª d. Por tanto, de Mi♯ a La♭ habrá una 4ª dd.
5. ESCALAS MAYORES
En el Capítulo 1 vimos que la escala de Do Mayor está formada por la siguiente sucesión de notas e intervalos:
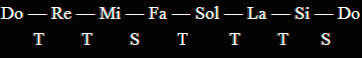
Escala de Do Mayor
La primera nota de la escala se llama Tónica (en nuestro ejemplo, el Do) y es habitual repetirla al final de la escala. El número de orden que tiene cada nota dentro de la escala se denomina grado de la escala y se representa con números romanos:
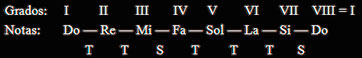
Escala de Do Mayor, con indicación de los grados
Los nombres de los grados son los siguientes:
|
Grado |
Nombre del Grado |
| I | Tónica |
| II | Supertónica |
| III | Mediante |
| IV | Subdominante |
| V | Dominante |
| VI | Superdominante |
| VII | Sensible |
| VIII |
Octava o Tónica |
Si quisiéramos construir una escala Mayor partiendo, por ejemplo, de la nota La, es decir, la escala de La Mayor, lo único que tendríamos que hacer es seguir la misma sucesión de tonos y semitonos que tenemos en la escala de Do Mayor, es decir, T T S T T T S:
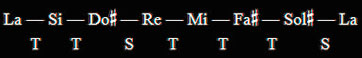
Escala de La Mayor
Por tanto, podemos definir la Escala Mayor como un conjunto de 7 notas caracterizadas por la sucesión de tonos y semitonos T T S T T T S. Otra forma equivalente de construir la escala Mayor consiste en buscar las notas que forman con la tónica intervalos de 2ª a 8ª Mayores o Justos.
En la escala de La Mayor observamos que hay 3 notas que llevan un sostenido (el Do, el Fa y el Sol), lo que es necesario para mantener la secuencia de tonos y semitonos. El número de sostenidos o bemoles que tiene una escala Mayor se conoce como Armadura. Así, se dice que la armadura de La Mayor tiene 3 sostenidos.
El orden en que aparecen los sostenidos en las escalas Mayores es siempre el mismo: Fa, Do, Sol, Re, La, Mi, Si (es decir, por intervalos de 5ª J). Esto significa que, en una escala Mayor que tenga 3 sostenidos, éstos corresponderán necesariamente a las notas Fa, Do y Sol, tal como hemos visto en la escala de La Mayor. Del mismo modo, si una escala Mayor contiene sólo 2 sostenidos, entonces corresponderán a las notas Fa y Do. Esto es lo que ocurre en la escala de Re Mayor:

Escala de Re Mayor
En el caso de los bemoles, éstos aparecen en orden inverso a los sostenidos, es decir, en el orden: Si, Mi, La, Re, Sol, Do, Fa (o sea, por intervalos de 4ª J). Así, en una escala que tenga 2 bemoles, éstos corresponderán necesariamente a las notas Si y Mi, lo cual ocurre en la escala de Si♭ Mayor:
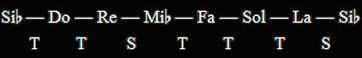
Escala de Si♭ Mayor
La formación de las escalas Mayores, el determinar qué armadura le corresponde a cada una de ellas o el saber en qué orden aparecen las tónicas cuando vamos aumentando o disminuyendo el número de sostenidos o de bemoles, son cuestiones complicadas que requieren bastante tiempo de estudio. Por este motivo, se ha dotado a la Rueda Armónica de un sistema muy sencillo para resolver todas estas cuestiones de una forma directa, a la vez que muy didáctica. Para ello, basta con girar convenientemente los dos discos de que consta este instrumento, como vamos a ver en el próximo capítulo.
6. ESCALAS MAYORES Y RUEDA ARMÓNICA
La obtención de las escalas Mayores con la Rueda Armónica se consigue, simplemente, girando sus dos discos entre sí, hasta hacer coincidir el signo  con la nota tónica deseada. El resto de las notas de la escala quedan señaladas, automáticamente, con el signo
con la nota tónica deseada. El resto de las notas de la escala quedan señaladas, automáticamente, con el signo ![]() . Como ejemplo, en la figura 6 se muestra la escala de Re Mayor.
. Como ejemplo, en la figura 6 se muestra la escala de Re Mayor.

Figura 6. Escala de Re Mayor.
Las líneas de COLOR AZUL OSCURO, por su parte, señalan la región de la Rueda Armónica que abarca esta escala (veremos su utilidad en el Capítulo 13). Para cualquier escala Mayor, esta región es un rectángulo curvado.
Las notas de la escala así señaladas están representadas en color negro (ya que este color siempre representa notas) y están colocadas siguiendo las relaciones de consonancia. No están, por tanto, ordenadas según su altura. Si queremos tener las notas de la escala ordenadas según su altura, debemos utilizar la notación en color rojo (aunque, como veremos en el Nivel 2, este color lo que representa son acordes). De esta manera, las notas aparecen a la derecha de unos números romanos, que indican los grados de la escala, tal como se aprecia en la figura 6. Al usar esta notación debemos prescindir de las letras y símbolos que hay a la derecha de las notas.
En la misma figura 6 podemos ver, al lado del grado I (Tónica), la armadura correspondiente a esta escala, es decir, 2 sostenidos. Si vamos girando entre sí los dos discos de que consta la Rueda Armónica, veremos aparecer las diferentes escalas, sus tónicas y sus armaduras. Así, podemos comprobar que, al aumentar el número de sostenidos o disminuir el de bemoles, las tónicas van apareciendo, precisamente, por quintas justas. Y, si disminuimos el número de sostenidos o aumentamos el de bemoles, las tónicas aparecen en sentido inverso, es decir, por cuartas justas.
Una propiedad interesante que tiene la escala Mayor es que, si representamos sus notas sobre una circunferencia, quedan todas ellas colocadas de forma correlativa y completando media circunferencia. Como ejemplo, en la figura 7 podemos ver este tipo de representación para las escalas de Re Mayor y La Mayor. Esto significa que las 7 notas de una escala Mayor pueden ordenarse por quintas justas, aunque para ello hay que comenzar por el grado IV, es decir, la Subdominante de la escala (Sol en el primer caso y Re en el segundo). El que estas notas estén conectadas por quintas justas indica el alto grado de consonancia que existe entre ellas. Nótese que, en la figura 7, se han descartado las enarmonías que no siguen la serie de intervalos de 5ª J.

Figura 7. Representación de las escalas de Re Mayor y La Mayor en una semicircunferencia.
Además, en esta representación puede verse claramente cómo van apareciendo las notas alteradas. Así, en la escala de Re Mayor, cuya armadura tiene 2 sostenidos, aparecen al final las dos notas Fa♯ y Do♯ (siguiendo el orden de los sostenidos). Y, al pasar de la escala de Re Mayor a la escala de La Mayor, vemos que se cambia el Sol por el Sol♯, como debe ocurrir, ya que la armadura de La Mayor tiene 3 sostenidos. De esta forma, se observa que los sostenidos van apareciendo por quintas justas, empezando por el Fa. Y, al aumentar el número de sostenidos de la armadura, las tónicas se suceden también por quintas justas. Del mismo modo, si representáramos escalas con bemoles, veríamos que éstos van apareciendo por cuartas justas, empezando por el Si; y que, al aumentar el número de bemoles, las tónicas se suceden también por cuartas justas.
El aprendizaje de las escalas lleva su tiempo. En primer lugar, debe aprenderse el orden de los sostenidos y de los bemoles. Y después, hay que saber cómo están relacionadas las armaduras con las tónicas. Para ello, son de utilidad las siguientes dos reglas, que podemos comprobar fácilmente si representamos las escalas de la misma forma que se ha hecho en la figura 7:
- En las armaduras que contienen sostenidos, la última nota con sostenido es la Sensible. Por ejemplo, en la armadura que tiene 3 sostenidos, éstos corresponden a Fa♯, Do♯ y Sol♯. Pues bien, el Sol♯ es la Sensible, luego la Tónica es La. Así, esta armadura corresponde a la escala de La Mayor.
- En las armaduras que contienen bemoles, la penúltima nota con bemol es la Tónica. Por ejemplo, en la armadura que tiene 5 bemoles, éstos corresponden a Si♭, Mi♭, La♭, Re♭ y Sol♭. Así, el Re♭ es la tónica y esta armadura corresponde a la escala de Re♭ Mayor.
A estas 2 reglas sólo falta añadir que la armadura que no contiene alteraciones corresponde a la escala de Do Mayor y la que tiene un bemol corresponde a la de Fa Mayor.Conociendo solamente la tónica y la armadura de una escala, ya hay que ser capaces de tocar la escala completa, tanto en sentido ascendente como descendente, hallando las notas mentalmente. Aunque la Rueda Armónica nos permite entender la formación de las escalas y resolver cualquier duda relacionada con ellas, no puede suplir la práctica necesaria para tocar las diferentes escalas con soltura.
Resulta difícil exagerar la importancia que tienen en Música las escalas Mayores. De hecho, todo el sistema de escritura musical está concebido para poder escribir cómodamente este tipo de escalas. Así, cuando uno aprende este sistema, puede comprobar que, dado un pentagrama con una clave cualquiera y una armadura también cualquiera, si no se utilizan alteraciones accidentales, todas las notas que se escriban corresponderán siempre a una cierta escala Mayor. Las notas que no pertenecen a esta escala, en cambio, llevarán alteraciones accidentales. De este modo, las alteraciones accidentales nos sirven para reconocer fácilmente las notas que no pertenecen a la escala Mayor considerada. Por otra parte, todos los instrumentos diatónicos (algunos tipos de flautas y armónicas, casi todos los instrumentos de juguete, etc.) contienen sólo las notas de una escala Mayor.
7. ESCALAS MENORES
Si, en una escala Mayor cualquiera, cambiamos de tónica pero mantenemos sus notas, lo que obtenemos es un nuevo Modo. Por ejemplo, si en la escala de Do Mayor, tomamos como tónica el Mi, resulta la escala: Mi, Fa, Sol, La, Si, Do, Re, Mi. Ésta no es una escala Mayor, ya que no sigue la sucesión de intervalos T T S T T T S, sino que es un modo asociado a la escala de Do Mayor. Hay, por tanto, 7 modos posibles asociados a cada escala Mayor, uno por cada nota de la escala que se elija como tónica. De hecho, la denominación “Mayor” es, precisamente, el nombre del modo cuya sucesión de intervalos es T T S T T T S.
La Música occidental ha evolucionado con el transcurso del tiempo hacia el denominado Sistema Bimodal, lo que significa que, de los 7 posibles modos, se ha quedado con dos: el Mayor y el menor. El modo menor es el que se obtiene tomando como tónica el grado VI de la escala Mayor. Así, a partir de la escala de Do Mayor, obtenemos la denominada “Escala de La menor natural”:

Escala de La menor natural, con indicación de los grados
Estas dos escalas, Do Mayor y La menor natural, se dice que son relativas una de la otra. De la misma manera, si partimos de la escala de Si♭ Mayor, obtenemos la escala de Sol menor natural. Y, si partimos de La Mayor, obtenemos la de Fa♯ menor natural.
En general, podemos definir la Escala menor natural como un conjunto de 7 notas caracterizadas por la siguiente sucesión de intervalos: T S T T S T T. Lógicamente, una escala Mayor y su relativa menor tienen asignada la misma armadura. En el capítulo 13 se verán las peculiaridades que presentan estos dos modos, Mayor y menor, y que hacen que prevalezcan sobre los demás.
La escala menor natural, sin embargo, adolece de un inconveniente: la distancia entre sus grados VII y VIII es de un tono y no de un semitono, como ocurre en la escala Mayor. Esto hace que, al tocar esta escala y pasar del grado VII al VIII, no dé la impresión de haber llegado al final de la escala. Musicalmente, se dice que el grado VII de la escala menor natural no tiene carácter de Sensible. Por este motivo, al grado VII de esta escala se le suele llamar Subtónica. Para evitar dicho inconveniente, es común en esta escala elevar un semitono el grado VII, lo que da lugar a la Escala menor armónica. La alteración necesaria para elevar dicho grado se dice que es accidental, debido a que no pertenece a la armadura. Las alteraciones que pertenecen a la armadura, por el contrario, se denominan propias.
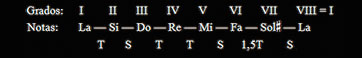
Escala de La menor armónica, con indicación de los grados
Ahora bien, en la escala menor armónica así construida aparece, entre sus grados VI y VII, un intervalo de 2ª A (es decir, 1,5 T), lo que produce un efecto extraño y poco natural, ya que se trata de un intervalo demasiado grande para estar entre dos grados consecutivos. Por ello, a veces se eleva también un semitono el grado VI de esta escala por medio de otra alteración accidental, lo que elimina este problema. Se tiene así la Escala menor melódica, en donde los intervalos entre dos grados consecutivos son siempre de un tono o un semitono.
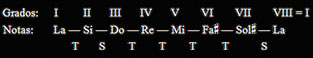
Escala de La menor melódica, con indicación de los grados
Finalmente, dado que el carácter de sensible asociado al grado VII sólo es necesario en la escala ascendente, pero no en la descendente, es también habitual el empleo de la escala menor melódica en sentido ascendente y la escala menor natural en sentido descendente. Esta escala se conoce, en ocasiones, como Escala menor mixta melódica, aunque a veces también recibe el nombre de, simplemente, “Escala menor melódica”, lo que puede dar lugar a confusiones. En este contexto, entenderemos por “Escala menor melódica” la que tiene los grados VI y VII elevados un semitono, tanto en sentido ascendente como descendente.
Mediante un procedimiento similar al visto con las escalas Mayores, la Rueda Armónica nos permite obtener también las notas de cualquier escala menor, sea ésta natural, armónica o melódica. Además, si nos fijamos en la notación en color rojo, veremos que cada armadura está al lado de dos “notas”, una de las cuales lleva la letra “m” de menor (en realidad, la notación en color rojo lo que representa son acordes, como veremos en el Nivel 2). Estas dos notas son, precisamente, las tónicas de la escala Mayor y su relativa menor que tienen asignada dicha armadura (la explicación de todo esto se verá en el Capítulo 12).
Como ejemplos de esto último, en la figura 8 se han señalado los siguientes casos: Con 2♭, las tónicas de Si♭ Mayor y Sol menor; con 2♯, las de Re Mayor y Si menor; con 3♯, las de La Mayor y Fa♯ menor; y, sin ninguna alteración, las de Do Mayor y La menor. Esta información debe ser suficiente para tocar todas estas escalas Mayores y menores, con todas las variantes de las escalas menores (natural, armónica, melódica y mixta melódica), hallando las notas mentalmente.
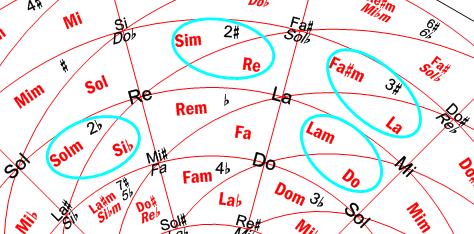
Figura 8. Tónicas de las escalas Mayores y sus relativas menores, con sus armaduras correspondientes.
8. MAPA DE TONALIDADES
El carácter Mayor o menor de una escala se conoce con el nombre de Modalidad o Modo. El que la Música occidental haya evolucionado hacia el denominado Sistema Bimodal significa que la mayoría de las obras o fragmentos musicales están compuestos, fundamentalmente, bien por la notas de una escala Mayor, bien por las de una escala menor.
Por otra parte, la altura a la que se encuentra una determinada escala Mayor o menor (es decir, si comienza por la nota Do, por La, por Mi♭, etc.) se denomina Tonalidad o Tono. En la práctica, sin embargo, el concepto de tonalidad suele incluir también al de modalidad. Así, se dice que tal obra o fragmento está escrito “en el tono de Do Mayor” o que tal otra lo está “en la tonalidad de Fa♯ menor”.
De esta manera, cada escala Mayor o menor tiene asociada una tonalidad con su mismo nombre. La diferencia entre la escala y la tonalidad es que, en la escala, las notas están ordenadas según su altura, mientras que, en la tonalidad, las notas pueden estar en cualquier orden e incluso pueden coincidir varias al mismo tiempo.
Tradicionalmente, la ordenación de las Tonalidades se ha realizado por medio del denominado Ciclo de Quintas. Esto significa, básicamente, que cada vez que pasamos de una tonalidad a otra que tiene un sostenido más o un bemol menos, la nueva tónica está a un intervalo de 5ª J con respecto a la tónica anterior. En la Rueda Armónica, este Ciclo de Quintas lo encontramos a lo largo de cualquiera de sus franjas circulares (figura 9).
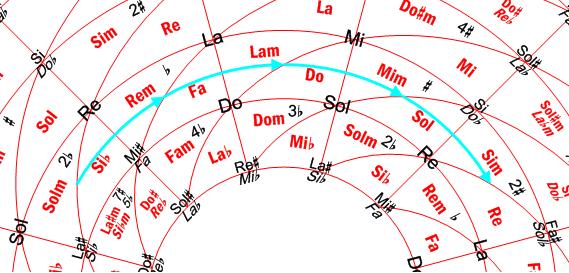
Figura 9. Ciclo de Quintas, a lo largo de una franja circular
El mismo Ciclo de Quintas sirve para determinar si dos tonalidades están próximas o lejanas. Así, las tonalidades relativas, como por ejemplo, Re Mayor y Si menor están muy próximas entre sí. También están próximas las tonalidades que se diferencian en una alteración en la armadura; por ejemplo, Fa Mayor y Do Mayor, o Fa Mayor y Si♭ Mayor.
Hay, sin embargo, un caso de tonalidades próximas entre sí que no se aprecia en el ciclo de quintas. Es el correspondiente al Cambio de Modo. Por ejemplo, es bien sabido que las tonalidades de Do Mayor y Do menor, o Mi menor y Mi Mayor, etc., son tonalidades que se encuentran muy próximas entre sí. Se dice también que son Tonalidades Paralelas. Este hecho, sin embargo, no es visible en el ciclo de quintas, debido a que hay 3 alteraciones de diferencia en sus armaduras. En la Rueda Armónica, por el contrario, sí se observa la proximidad entre las tonalidades paralelas. Éstas se encuentran una a continuación de otra en la dirección radial (figura 10). Además, dado que cada radio comienza y termina en una misma nota, al llegar a uno de sus extremos, podemos continuar por el otro, cerrando también un ciclo en esta dirección.
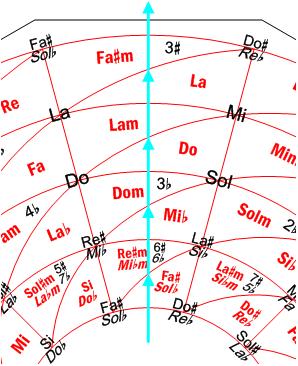
Figura 10. Cambios de Modo cíclicos, en la dirección radial.
Así, mientras el ciclo de quintas muestra las tonalidades a lo largo de una línea (o sea, en una dimensión), la Rueda Armónica las muestra en una superficie (es decir, en dos dimensiones). Debido a ello, la Rueda Armónica ofrece una visión completa y panorámica de las relaciones existentes entre todas las Tonalidades. Esta es, de hecho, una de las características más importantes de la Rueda Armónica: el llamado MAPA DE LAS TONALIDADES.


